数据结构与算法之美

重点掌握

数组、链表、栈、队列、散列表、二叉树、堆、跳表、图、Trie
递归、排序、二分查找、搜索、哈希算法、贪心算法、分治算法、回溯算法、动态规划、字符串匹配算法

复杂度分析

时间复杂度

只关注循环执行次数最多的一段代码
加法法则：总复杂度等于量级最大的那段代码的复杂度
乘法法则：嵌套代码的复杂度等于嵌套内外代码复杂度的乘积

常见时间复杂度

常量 O(1)
对数 O(logn)
线性 O(n)
线性对数 O(nlogn)
平方 O(n^2)
指数 O(2^n)
阶乘 O(n!)

空间复杂度

算法的存储空间与数据规模之间的增长关系。

1
2
3
4


// O(n)
void print(int n) {
    int[] a = new int[n];
}

分析手法

最好情况时间复杂度（best case time complexity）
最坏情况时间复杂度（worst case time complexity）
平均情况时间复杂度（average case time complexity）
均摊时间复杂度（amortized time complexity）

数据结构与算法

数组

为何数组坐标从 0 开始？下标的更准确说法应该是: 偏移位数

1
2
3


int a[];
// 基址 + 偏移量
a[k]_address = base_address + k * type_size;

BinarySearch

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


def binary_search(arr, t) -> int:
    if not arr:
        return -1
    l, r = 0, len(arr)
    while l <= r:
        m = l + (r - l) // 2
        if arr[m] > t:
            r = m
        elif arr[m] < t:
            l = m + 1
        else:
            return m
    return l

LinkedList

理解指针或引用的具体含义
警惕指针丢失和内存泄漏
利用哨兵减少实现难度【dummy head 节点】
重点留意边界处理
举例画图，辅助思考
多写多练

1
2
3
4


class ListNode:
    def __init__(self, val=0, next=None):
        self.val = val
        self.next = next

Edge Case

如果链表为空时，代码是否能正常工作？
如果链表只包含一个结点时，代码是否能正常工作？
如果链表只包含两个结点时，代码是否能正常工作？
代码逻辑在处理头结点和尾结点的时候，是否能正常工作？

单链表反转

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


class Solution:
    def reverseList(self, head: ListNode) -> ListNode:
        prev = None
        cur = head
        while cur:
            nxt = cur.next
            cur.next = prev
            prev = cur
            cur = nxt
        return prev

链表中环的检测

1
2
3
4
5
6
7
8


def hasCycle(self, head: ListNode) -> bool:
    slow, fast = head, head
    while fast and fast.next:
        slow = slow.next
        fast = fast.next.next
        if slow == fast:
            return True
    return False

两个有序的链表合并

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


def mergeTwoLists(self, list1: ListNode, list2: ListNode) -> ListNode:
    dummy = cur = ListNode(-1)
    while list1 and list2:
        if list1.val >= list2.val:
            cur.next = list2
            list2 = list2.next
        else:
            cur.next = list1
            list1 = list1.next
        cur = cur.next
    cur.next = list1 or list2

    return dummy.next

寻找中间节点

1
2
3
4
5
6
7
8
9


def middleNode(self, head: Optional[ListNode]) -> Optional[ListNode]:
    slow, fast = head, head
    while fast and fast.next:
        slow = slow.next
        fast = fast.next.next
    # 偶数返回右侧
    if fast and fast.next:
        return slow.next
    return slow

Stack

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22


class MyStack:
    def __init__(self, cap):
        self.data = [0] * cap
        self.cap = cap
        self.index = -1

    def push(self, val) -> bool:
        if self.index >= self.cap - 1:
            return False
        self.index += 1
        self.data[self.index] = val
        return True

    def pop(self) -> Optional[int]:
        if self.index < 0:
            return None
        ret = self.data[self.index]
        self.index -= 1
        return ret

    def empty(self) -> bool:
        return self.index < 0

Queue

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27


# 循环队列会浪费一个数组的存储空间。
class CircularQueue:
    def __init__(self, cap):
        self.data = [0] * cap
        self.cap = cap
        self.head = 0
        self.tail = 0

    def enqueue(self, val) -> bool:
        if self.full():
            return False
        self.data[self.tail] = val
        self.tail = (self.tail + 1) % self.cap
        return True

    def dequeue(self) -> Optional[int]:
        if self.empty():
            return None
        ret = self.data[self.head]
        self.head = (self.head + 1) % self.cap
        return ret

    def full(self) -> bool:
        return (self.tail + 1) % self.cap == self.head

    def empty(self) -> bool:
        return self.head == self.tail

递归 Recursion

一个问题的解可以分解为几个子问题的解
这个问题与分解之后的子问题，除数据规模外，求解思路一致
存在递归终止条件

写递归代码的关键就是找到如何将大问题分解为小问题的规律，并且基于此写出递推公式，然后再推敲终止条件，最后将递推公式和终止条件翻译成代码。

1
2
3
4


def fib(n):
    if n == 1 or n == 2:
        return 1
    return fib(n-1) + fib(n-2)

排序

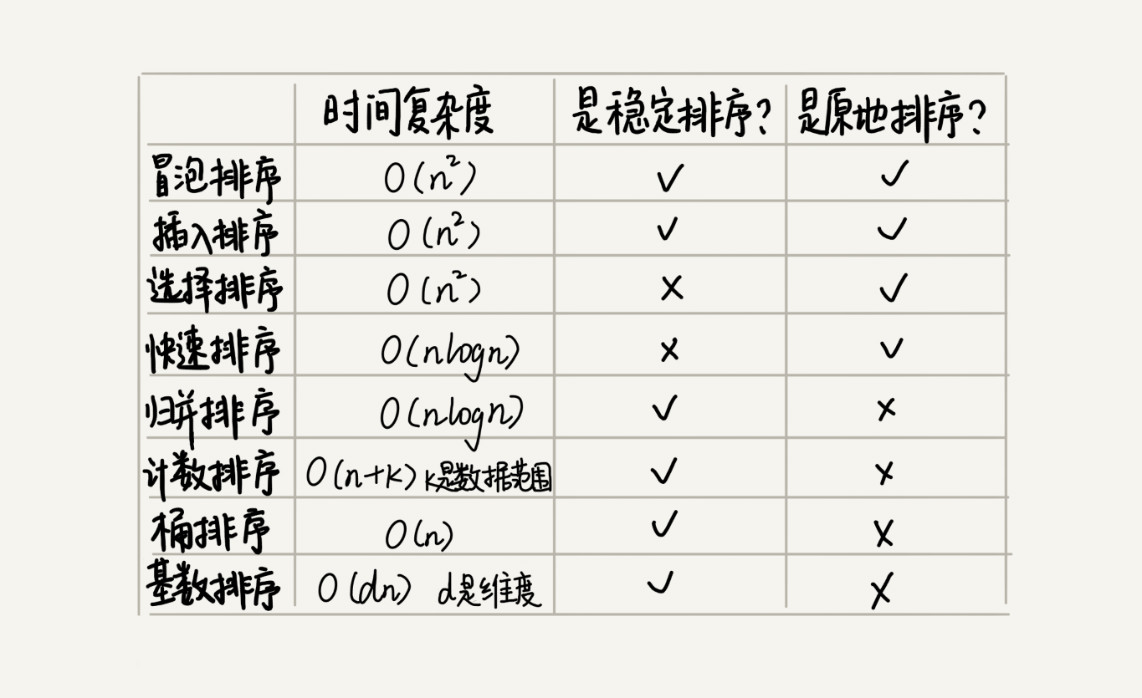
有序度是数组中具有有序关系的元素对的个数。满有序度: n*(n-1)/2，逆序度 = 满有序度 - 有序度。

最好情况、最坏情况、平均情况时间复杂度
时间复杂度的系数、常数、低阶
比较次数和交换（或移动）次数

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96


# O(n^2), stable
def bubble_sort(nums):
    for i in range(0, len(nums)):
        # return early
        sorted_flag = False
        for j in range(i+1, len(nums)):
            if nums[i] > nums[j]:
                nums[i],nums[j] = nums[j],nums[i]
                # data exchange occurred
                sorted_flag = True
        if not sorted_flag:
            break

# O(n^2), stable
def insertion_sort(nums):
    for i in range(1, len(nums)):
        val = nums[i]
        # comparison with prev one
        j = i - 1
        # move greater ones backwards
        while j >= 0 and nums[j] > val:
            nums[j+1] = nums[j]
            j -= 1
        # reside the small one
        nums[j+1] = val

# O(n^2), unstable
def selection_sort(nums):
    for i in range(0, len(nums) - 1):
        mini = i
        for j in range(i+1, len(nums)):
            if nums[mini] > nums[j]:
                mini = j
        nums[mini], nums[i] = nums[i], nums[mini]

# O(nlogn), stable, extra space O(n)
def merge_sort(nums: List[int]):
    def merge(arr1: List[int], arr2: List[int]) -> List[int]:
        ret = []
        i,j = 0, 0
        while i < len(arr1) and j < len(arr2):
            if arr1[i] > arr2[j]:
                ret.append(arr2[j])
                j += 1
            else:
                ret.append(arr1[i])
                i += 1
        while i < len(arr1):
            ret.append(arr1[i])
            i += 1
        while j < len(arr2):
            ret.append(arr2[j])
            j += 1
        return ret
    if len(nums) <= 1:
        return nums
    m = len(nums) // 2
    left = merge_sort(nums[:m])
    right = merge_sort(nums[m:])

    return merge(left, right)

# quick sort
def quick_sort(arr):
    if len(arr) <= 1:
        return arr
    else:
        pivot = arr[len(arr) // 2]
        left = [x for x in arr if x < pivot]
        middle = [x for x in arr if x == pivot]
        right = [x for x in arr if x > pivot]
        return quick_sort(left) + middle + quick_sort(right)

# in-place version
def quicksort(arr, low, high):
    if low < high:
        # Partition the array and get the pivot index
        pivot_index = partition(arr, low, high)
        # Recursively sort the elements before and after partition
        quicksort(arr, low, pivot_index - 1)
        quicksort(arr, pivot_index + 1, high)

def partition(arr, low, high):
    # Select the pivot (here we choose the last element as the pivot)
    pivot = arr[high]
    # Initialize the index of the smaller element
    i = low - 1
    # Rearrange the elements in relation to the pivot
    for j in range(low, high):
        if arr[j] <= pivot:
            i += 1
            # Swap elements if the current element is smaller than or equal to the pivot
            arr[i], arr[j] = arr[j], arr[i]
    # Swap the pivot element with the element at i+1 position
    arr[i + 1], arr[high] = arr[high], arr[i + 1]
    return i + 1

bucket sort
counting sort
radix sort

桶排序的实践思路：假设经过扫描之后我们得到，订单金额最小是 1 元，最大是 10 万元。我们将所有订单根据金额划分到 100 个桶里，第一个桶我们存储金额在 1 元到 1000 元之内的订单，第二桶存储金额在 1001 元到 2000 元之内的订单，以此类推。每一个桶对应一个文件，并且按照金额范围的大小顺序编号命名（00，01，02…99）。

二分查找

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


def binary_search(nums, t) -> int:
    nums.sort()
    l,r = 0, len(nums)
    while l <= r:
        m = l + (r-l) // 2
        if nums[m] > t:
            r = m - 1
        elif nums[m] < t:
            l = m + 1
        else:
            return m
    # -1 to indicate not found
    # l to indicate insertion position (if no duplicates)
    return l

变形问题

查找第一个等于给定值的元素
查找最后一个等于给定值的元素
查找第一个大于等于给定值的元素
查找最后一个小于等于给定值的元素
bisect_left 在 = 的时候，无限左移 l = m -1
bisect_right 在 = 的时候，无限右移 r = l + 1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33


public int bsearch(int[] a, int n, int value) {
  int low = 0;
  int high = n - 1;
  while (low <= high) {
    int mid =  low + ((high - low) >> 1);
    if (a[mid] > value) {
      high = mid - 1;
    } else if (a[mid] < value) {
      low = mid + 1;
    } else {
      if ((mid == 0) || (a[mid - 1] != value)) return mid;
      else high = mid - 1;
    }
  }
  return -1;
}

public int bsearch(int[] a, int n, int value) {
  int low = 0;
  int high = n - 1;
  while (low <= high) {
    int mid =  low + ((high - low) >> 1);
    if (a[mid] > value) {
      high = mid - 1;
    } else if (a[mid] < value) {
      low = mid + 1;
    } else {
      if ((mid == n - 1) || (a[mid + 1] != value)) return mid;
      else low = mid + 1;
    }
  }
  return -1;
}

Skip List

插入时，为了维护索引与原始数据之间的平衡，引入一个随机函数，来决定将此节点插入到哪几级索引。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65


class Skiplist {
    class Node {
        int val;
        Node next, down;
        public Node(int val, Node next, Node down) {
            this.val = val;
            this.next = next;
            this.down = down;
        }
    }
    Node head = new Node(-1, null, null);
    Random rand = new Random();
    public Skiplist() {

    }

    public boolean search(int target) {
        Node cur = head;
        while (cur != null) {
            while (cur.next != null && cur.next.val < target) {
                cur = cur.next;
            }
            if (cur.next != null && cur.next.val == target) return true;
            cur = cur.down;
        }
        return false;
    }

    public void add(int num) {
        Stack<Node> stack = new Stack<>();
        Node cur = head;
        while (cur != null) {
            while (cur.next != null && cur.next.val < num) {
                cur = cur.next;
            }
            stack.push(cur);
            cur = cur.down;
        }
        boolean insert = true;
        Node down = null;
        while (insert && !stack.isEmpty()) {
            cur = stack.pop();
            cur.next = new Node(num, cur.next, down);
            down = cur.next;
            insert = rand.nextDouble() < 0.5;
        }
        if (insert) head = new Node(-1, null, head);
    }

    public boolean erase(int num) {
        Node cur = head;
        boolean found = false;
        while (cur != null) {
            while (cur.next != null && cur.next.val < num) {
                cur = cur.next;
            }
            if (cur.next != null && cur.next.val == num) {
                found = true;
                cur.next = cur.next.next;
            }
            cur = cur.down;
        }
        return found;
    }
}

Hash

开放寻址法：Hash 冲突时，遍历寻找下一个空闲的位置，将数据填进去【删除数据时不能直接删除，需要采取特殊方式，如添加 DELETED 标志，防止开放寻址时无法找到数据】【适合数据量小，负载因子低的场景】
拉链法：Hash 冲突时，转化成链表【1 次 hash 后，再直接对比 key 值】

1
2
3
4


public int hash(){
    int h = this.key.hashCode();
    return (h ^ (h >>> 16)) | (this.capacity - 1);
}

Hash 算法的应用

生成唯一标识
校验数据的完整性和正确性【分片下载】
安全加密
散列函数
负载均衡
数据分片
分布式存储

Tree

前序位置的代码只能从函数参数中获取父节点传递来的数据，而后序位置的代码不仅可以获取参数数据，还可以获取到子树通过函数返回值传递回来的数据。

一旦发现题目和子树有关，那大概率要给函数设置合理的定义和返回值，在后序位置写代码了。

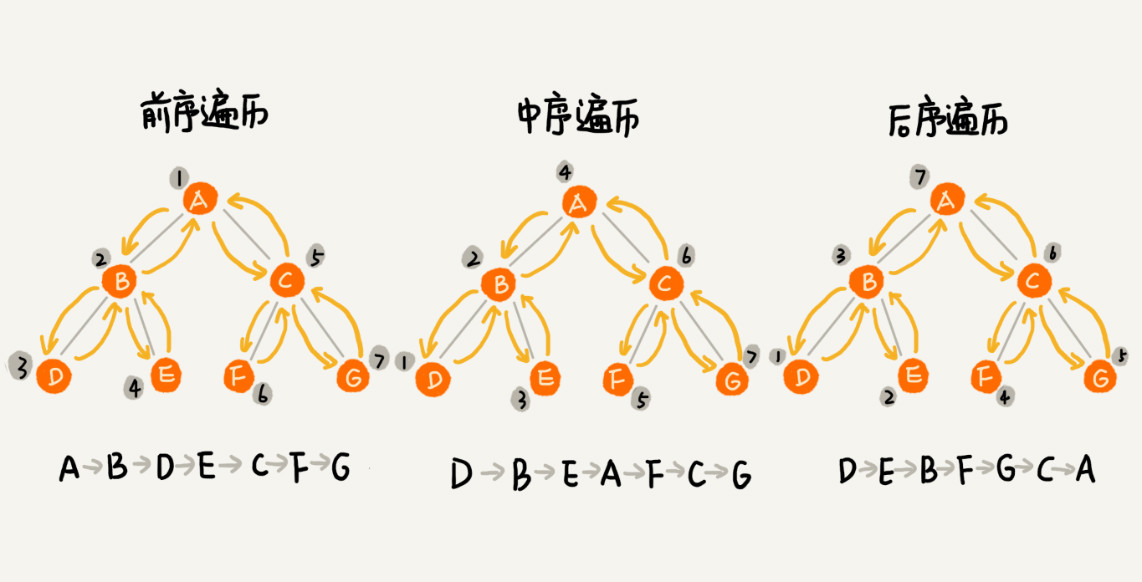
遍历

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24


void printLevel(TreeNode root) {
    helper(root, 1);
}

void helper(TreeNode node, int level) {
    if (node == null) {
        return;
    }
    // prev
    print(node.val, level);
    helper(node.left, level+1);
    helper(node.right, level+1);
}

int coundSubNodes(TreeNode root) {
    if (root == null) {
        return 0;
    }
    int l = countSubNodes(root.left);
    int r = countSubNodes(root.right);

    // the final result relies on all sub-tree result
    return 1 + l + r;
}

二叉树
满二叉树
完全二叉树【当用数组表示时，无需多余空间，可以填充满整个数组】【i, 2*i left, 2*i right】

遍历规则：

前序遍历: cur -> left -> right
中序遍历: left -> cur -> right
后续遍历: left -> right -> cur

红黑树

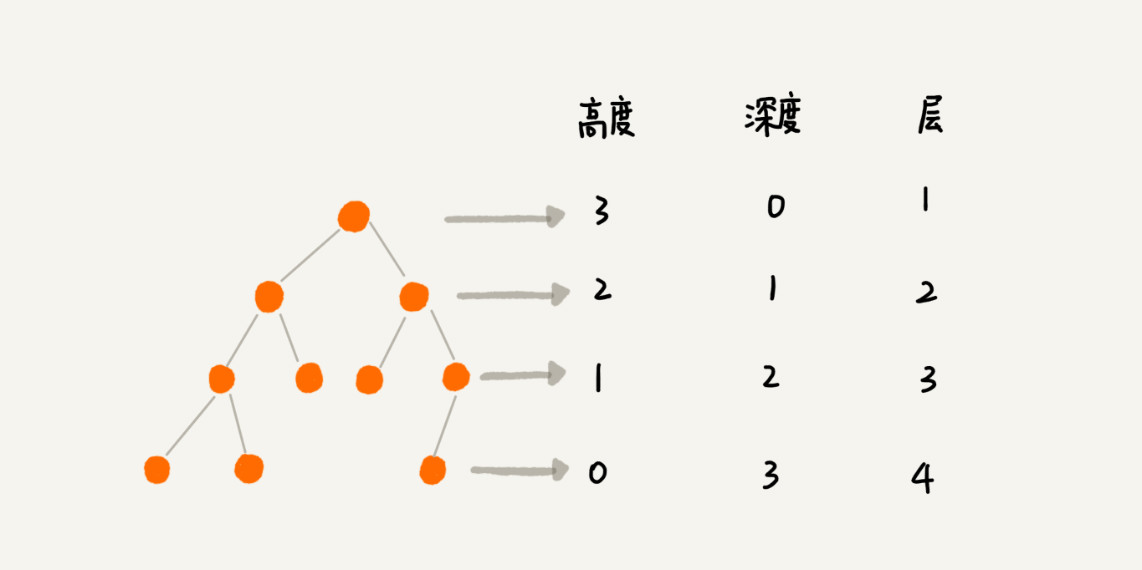
平衡二叉树的严格定义是这样的：二叉树中任意一个节点的左右子树的高度相差不能大于 1。

平衡二叉查找树中“平衡”的意思，其实就是让整棵树左右看起来比较“对称”、比较“平衡”，不要出现左子树很高、右子树很矮的情况。这样就能让整棵树的高度相对来说低一些，相应的插入、删除、查找等操作的效率高一些。

根节点是黑色的；
每个叶子节点都是黑色的空节点（NIL），也就是说，叶子节点不存储数据；
任何相邻的节点都不能同时为红色，也就是说，红色节点是被黑色节点隔开的；
每个节点，从该节点到达其可达叶子节点的所有路径，都包含相同数目的黑色节点；

字符串搜索算法

BF 暴力查询
RK 子串 hash，hash 匹配后再逐个判断
BM BM 算法包含两部分，分别是坏字符规则（bad character rule）和好后缀规则（good suffix shift）。
KMP 在模式串和主串匹配的过程中，当遇到坏字符后，对于已经比对过的好前缀，能否找到一种规律，将模式串一次性滑动很多位？

Trie

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32


class TrieNode:
    def __init__(self, c, is_word=False):
        self.c = c
        self.is_word = is_word
        self.children = [None] * 26


class Trie:
    def __init__(self):
        self.root = TrieNode("#")

    def insert(self, s: str):
        if not s:
            return
        node = self.root
        for i in range(len(s)):
            idx = ord(s[i]) - ord("a")
            node.children[idx] = TrieNode(s[i])
            node = node.children[idx]
        node.is_word = True

    def find(self, s: str) -> bool:
        if not s:
            return False
        node = self.root
        for i in range(len(s)):
            idx = ord(s[i]) - ord("a")
            if node.children[idx]:
                node = node.children[idx]
            else:
                return False
        return node.is_word

Greedy

分糖果
区间覆盖

概览

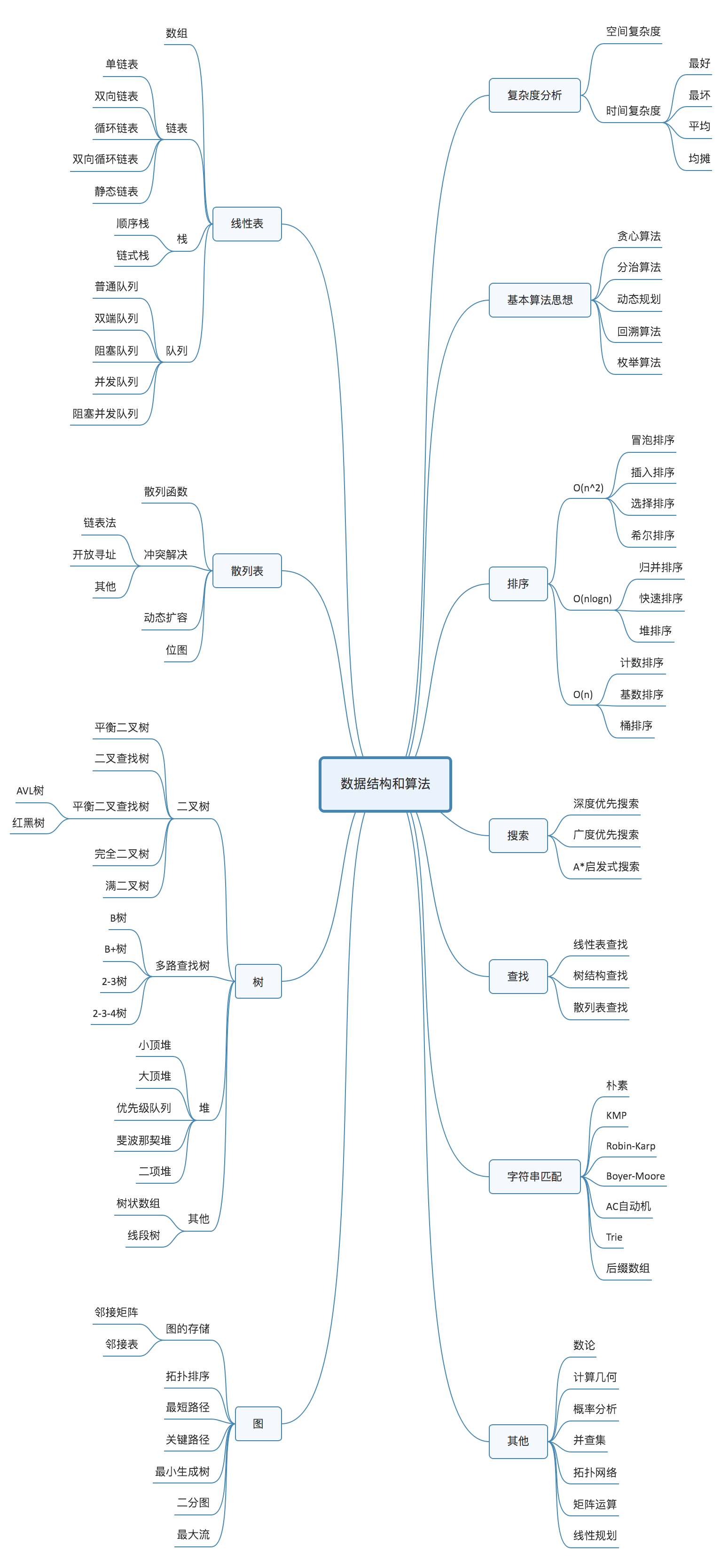
总结

Problems

对 D，a，F，B，c，A，z 这个字符串进行排序，要求将其中所有小写字母都排在大写字母的前面，但小写字母内部和大写字母内部不要求有序

用两个指针 a、b：a 指针从头开始往后遍历，遇到大写字母就停下，b 从后往前遍历，遇到小写字母就停下，交换 a、b 指针对应的元素；重复如上过程，直到 a、b 指针相交。

对于小写字母放前面，数字放中间，大写字母放后面，可以先将数据分为小写字母和非小写字母两大类，进行如上交换后再在非小写字母区间内分为数字和大写字母做同样处理

References

数据结构与算法之美 - 极客时间
《算法导论》